КИХ-фильтры

КИХ-фильтры |
Предыдущая Содержание Следующая |

|
|
КИХ фильтры полезны тогда, когда необходим высокий порядок фильтра и/или требуется сохранения фазовых отношений.
При определённых соотношениях между частотой дискретизации, частотой среза фильтра и его порядком крайние коэффициенты равны нулю. В этом случае теряются крайние отсчёты и имеет смысл изменить порядок фильтра, обычно в сторону понижения.
Расчёт фильтра сводится к расчёту его импульсной характеристики.
Для ФНЧ это функция вида sin(x)/x. Для ФВЧ это функция вида -sin(x)/x, в точке 0: 1 - sin(x)/x. Для полосового фильтра это разность импульсных характеристик ФВЧ и ФНЧ. Для режекторного фильтра это разность импульсных характеристик ФНЧ и ФВЧ, в точке 0: 1 - diff.
Для уменьшения амплитуд боковых лепестков используется взвешивание оконной функцией.
Импульсные характеристики фильтров:
Расчёт фильтра с произвольной АЧХВыбираем порядок фильтра и число точек для описания АЧХ в диапазоне 0 ... частота дискретизации/2. При этом порядок фильтра не должен превышать удвоенное число точек АЧХ. Для расчёта используем БПФ, поэтому число точек описания АЧХ должно быть степенью двойки. Выбираем порядок фильтра: 11. Число точек АЧХ: 8. Описываем АЧХ фильтра, фильтр нижних частот. Числа выбраны немного отличными от 1, чтобы лучше проиллюстрировать дальнейшие манипуляции:
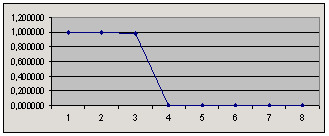 АЧХ фильтра
Формируем буфер для обратного БПФ. Он имеет длину в 4 раза больше числа точек описания АЧХ. Каждое значение состоит из двух чисел, чётные - косинусные составляющие, нечётные - синусные. Кроме того, значения заносятся симметрично относительно центра. Так как предполагается иметь нулевой сдвиг по фазе, синусные составляющие нулевые.
Выполняем обратное БПФ.
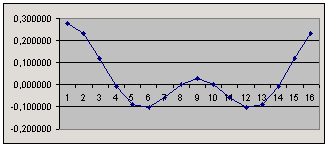 Чётные элементы после БПФ
Чётные элементы массива содержат импульсную характеристику, смещённую на половину длины буфера. Забираем необходимое количество значений (11) и получаем импульсную характеристику фильтра.
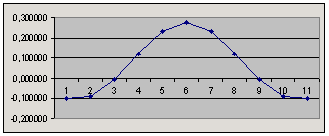 Импульсная характеристика фильтра
Применяем оконную функцию для уменьшения боковых лепестков и получаем окончательный вид импульсной характеристики фильтра.
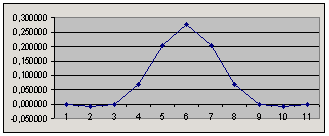 Импульсная характеристика после взвешивания оконной функцией
Расчёт методом Паркса-МаклелланаСмотрите: http://en.wikipedia.org/wiki/Parks-McClellan_filter_design_algorithm Метод позволяет рассчитать оптимальный в минимаксном смысле фильтр (фильтр Чебышева). РеализацияВ данной реализации число отводов фильтра полагается равным порядку фильтра, а не +1, просто для удобства.
/** * КИХ фильтр */ public class FIR { public static final byte RECTANGULAR = 0;// Rectangular window function public static final byte BARTLETT = 1;// Bartlett (triangular) window public static final byte HANNING = 2;// Hanning window public static final byte HAMMING = 3;// Hamming window public static final byte BLACKMAN = 4;// Blackman window public static final byte BLACKMAN_HARRIS = 5;// Blackman-Harris window public static final byte BLACKMAN_NUTTAL = 6;// Blackman-Nuttal window public static final byte NUTTAL = 7;// Nuttal window // public static final byte OFF = 0; public static final byte LOWPASS = 1; public static final byte HIGHPASS = 2; public static final byte BANDSTOP = 3;// NOTCH public static final byte BANDPASS = 4; // private static final int GRIDDENSITY = 16; private static final int MAXITERATIONS = 40; // private short[] m_delay; private double[] m_fir; // public FIR() {} /** * получить коэффициент заданного типа окна * @param i - индекс * @param n - размер окна * @param type - тип окна * @return коэффициент */ static double getWindow(int i, int n, byte window) { if( window == BARTLETT ) {// устраняем нулевые значения double a = i - (n - 1) / 2.0; if( a < 0 ) a = -a; return 2.0 / n * (n / 2.0 - a); } else if( window == HANNING )// устраняем нулевые значения return 0.5 - 0.5 * Math.cos(Math.PI / n * (1.0 + 2.0 * i)); if( window == BLACKMAN ) {// устраняем нулевые значения double a = Math.PI / n * (1.0 + 2.0 * i); return 0.5 * (1.0 - 0.16 - Math.cos(a) + 0.16 * Math.cos(2.0 * a)); } else { double a = 2.0 * Math.PI * i / (n - 1); if( window == HAMMING ) return 0.54 - 0.46 * Math.cos( a ); else if( window == BLACKMAN_HARRIS ) return 0.35875 - 0.48829 * Math.cos(a) + 0.14128 * Math.cos(2.0 * a) - 0.01168 * Math.cos(3.0 * a); else if( window == BLACKMAN_NUTTAL ) return 0.35819 - 0.4891775 * Math.cos(a) + 0.1365995 * Math.cos(2.0 * a) - 0.0106411 * Math.cos(3.0 * a); else if( window == NUTTAL ) return 0.355768 - 0.487396 * Math.cos(a) + 0.144232 * Math.cos(2.0 * a) - 0.012604 * Math.cos(3.0 * a); } //if( type == RECTANGULAR ) return 1.0; } /** * инициализация параметров * @param type - тип фильтра * @param window - окно * @param order - порядок фильтра * @param f1 - частота ФНЧ и ФВЧ фильтра * @param f2 - верхняя частота для полосового и режекторного фильтра * @param sampleRate - частота дискретизации */ public void init(byte type, byte window, short order, int f1, int f2, int sampleRate) { m_fir = new double[order]; m_delay = new short[order];// создаём и обнуляем буфер данных if( order == 1 ) { m_fir[0] = 1.0; return; } final int n2 = order / 2; double w = 2.0 * Math.PI * (double)f1 / (double)sampleRate; double sum = 0; /* расчёт симметричной характеристики для ФНЧ double c = (order - 1) / 2.0; if( (order&1) != 0 ) { m_fir[n2] = w * getWindow( n2, order, BLACKMAN ); sum += m_fir[n2]; } for( int i = 0; i < n2; i++ ) { double d = (double)i - c; m_fir[i] = Math.sin(w * d) / d * getWindow( i, order, window ); sum += m_fir[i]; sum += m_fir[i]; } // нормализация if( (order&1) != 0 ) m_fir[n2] /= sum; for( int i = 0; i < n2; i++ ) m_fir[i] = m_fir[order - i - 1] = m_fir[i] / sum; */ for( int i = 0; i < order; i++ ) { final int d = i - n2; m_fir[i] = ((d == 0) ? w : Math.sin(w * d) / d) * getWindow(i, order, window); sum += m_fir[i]; } // нормализация for( int i = 0; i < order; i++ ) { m_fir[i] /= sum; } // if( type == LOWPASS ) return; else if( type == HIGHPASS ) { for( int i = 0; i < order; i++ ) { m_fir[i] = -m_fir[i]; } m_fir[n2] += 1.0; return; } else {// если полосовой или режекторный фильтр // расчитываем верхнюю частоту double[] hf = new double[order]; w = 2.0 * Math.PI * (double)f2 / (double)sampleRate; sum = 0; for( int i = 0; i < order; i++ ) { final int d = i - n2; hf[i] = ((d == 0) ? w : Math.sin(w * d) / d) * getWindow(i, order, window); sum += hf[i]; } // нормализация for( int i = 0; i < order; i++ ) { hf[i] /= sum; } // инвертируем и объединяем с ФНЧ for( int i = 0; i < order; i++ ) { m_fir[i] -= hf[i]; } m_fir[n2] += 1.0; if( type == BANDSTOP ) return; else if( type == BANDPASS ) { for( int i = 0; i < order; i++ ) { m_fir[i] = -m_fir[i]; } m_fir[n2] += 1.0; } } } /** * инициализация параметров * @param env - огибающая фильтра, коэффициенты передачи. * длина массива должна быть степенью числа 2 * @param order - порядок фильтра, меньше удвоенной длины массива огибающей * @param window - тип окна */ public boolean init(double[] env, short order, byte window) { if( order >= (env.length << 1) ) { System.out.println("filter order must be lower than filter envelope length"); return false; } if( (env.length & (env.length - 1)) != 0 ) { System.out.println("filter envelope length must be power of 2"); return false; } // расчитываем импульсную характеристику double[] buf = new double[env.length << 2]; // обнуляем фазу и центральный элемент (в java буфер уже обнулён) //for( int i = 1; i < (env.length << 2); i += 2 ) { buf[i] = 0.0; } //buf[env.length << 1] = 0.0; // готовим симметричный буфер buf[0] = env[0]; for( int i = 1; i < env.length; i++ ) { buf[i << 1] = buf[(env.length << 2) - (i << 1)] = env[i]; } // обратное БПФ int power = 0; for( int i = 1; i < (env.length << 2); power++ ) { i = i << 1; } FFT.realFastFourierTransform( env, power, true ); // забираем импульсную характеристику и применяем оконную функцию m_fir = new double[order]; for( int i = 0; i < order; i++ ) { final int m = (i - (order >> 1)) << 1; m_fir[i] = buf[m & ((env.length << 2) - 1)] * getWindow(i, order, window); } // создаём и обнуляем буфер данных m_delay = new short[order];// в java уже обнулён //for( int i = 0; i < order; i++ ) { m_delay[i] = 0; } return true; } /************************************************************************** * Алгоритм Паркса-Макклеллана для расчёта КИХ фильтра (версия на Си) * Copyright (C) 1995 Jake Janovetz (janovetz@coewl.cen.uiuc.edu) * Converted to Java by Iain A Robin, June 1998 *************************************************************************/ /** * оцениваем необходимый порядок фильтра с помощью формулы Кайзера * @param trband - нормализованная переходная полоса фильтра * @param atten_dB - степень подавления в дБ. * @param ripple_dB - пульсации в полосе пропускания дБ */ public static int estimatedOrder(double trband, double atten_dB, double ripple_dB) { double deltaP = 0.5 * (1.0 - Math.pow( 10.0, -0.05 * ripple_dB ) ); double deltaS = Math.pow( 10.0, -0.05 * atten_dB ); return Math.round( (float)((-10.0 * Math.log10(deltaP * deltaS) - 13)/(14.6 * trband)) ); } /******************* * createDenseGrid *================= * Создёт плотную сетку частот из указанных диапазонов. * Также создаёт функцию Требуемого Частотного Отклика (d[]) и * Весовую функцию (w[]) этой сетки * * @param r - число коэффициентов фильтра / 2 * @param numtaps - число коэффициентов в результирующем фильтре * @param numband - число диапазонов, заданных пользователем * @param bands - число границ диапазонов, заданных пользователем [2*numband] * @param des - желаемый отклик в каждом диапазоне [numband] * @param weight - вес в каждом диапазоне [numband] * @param symmetry - симметрия фильтра - используется для проверки сетки * @param gridSize - число элементов в плотной сетке частот * * @return grid - частоты (от 0 до 0.5) плотной сетки [gridSize] * @return d - желаемый отклик плотной сетки [gridSize] * @return w - весовая функция плотной сетки [gridSize] *******************/ private static void createDenseGrid(int r, int numtaps, int numband, double bands[], double des[], double weight[], int gridSize, double grid[], double d[], double w[], boolean is_symmetry) { final double delf = 0.5 / (GRIDDENSITY * r);
// Для дифференциатора, гильберта, // симметрия является нечётной и grid[0] = max( delf, band[0] ) if( ! is_symmetry && (delf > bands[0] ) ) bands[0] = delf;
for( int band = 0, j = 0; band < numband; band++ ) { int band2 = band << 1; grid[j] = bands[band2]; double lowf = bands[band2]; double highf = bands[++band2]; final int k = (int)Math.round( (highf - lowf) / delf ); for( int i = 0; i < k; i++ ) { d[j] = des[band]; w[j] = weight[band]; grid[j] = lowf; lowf += delf; j++; } grid[j - 1] = highf; }
// Аналогично вышесказанному, если симметрия нечётна, // последний указатель сетки не может быть .5 // - но, если число отводов чётное, оставляем указатель сетки в .5 if( ! is_symmetry && (grid[gridSize - 1] > (0.5 - delf)) && ((numtaps & 1) != 0)) { grid[gridSize - 1] = 0.5 - delf; } } /******************** * initialGuess *============== * Размещает Экстремальные Частоты равномерно по всей плотной сетке. * * @param r - число коэффициентов фильтра / 2 * @param gridSize - число элементов в плотной сетке частот * * @return ext[] - указатели на экстремумы в плотной сетке частот [r+1] ********************/ private static void initialGuess(int r, int ext[], int gridSize) { for( int i = 0; i <= r; i++ ) ext[i] = i * (gridSize - 1) / r; } /*********************** * calcParms *=========== * * @param r - число коэффициентов фильтра / 2 * @param ext - Указатели на экстремумы в плотной сетке частот [r+1] * @param grid - частоты (от 0 до 0.5) плотной сетки [gridSize] * @param d - желаемый отклик плотной сетки [gridSize] * @param w - весовая функция плотной сетки [gridSize] * * @return ad - 'b' в книге Оппенгейма & Шафера [r+1] * @return x - [r+1] * @return y - 'C' в книге Оппенгейма & Шафера [r+1] ***********************/ private static void calcParms(int r, int ext[], double grid[], double d[], double w[], double ad[], double x[], double y[]) { double denom, numer;
// Расчитываем x[] for( int i = 0; i <= r; i++ ) x[i] = Math.cos( 2.0 * Math.PI * grid[ext[i]] );
// Расчитываем ad[] - уравнение 7.132 в книге Оппенгейма & Шафера final int ld = (r - 1) / 15 + 1;// Переход вокруг, чтобы избежать ошибок округления for( int i = 0; i <= r; i++ ) { denom = 1.0; final double xi = x[i]; for( int j = 0; j < ld; j++ ) { for( int k = j; k <= r; k += ld ) if( k != i ) denom *= 2.0 * (xi - x[k]); } if( Math.abs( denom ) < 0.00001 ) denom = 0.00001; ad[i] = 1.0 / denom; }
// Расчитываем delta - уравнение 7.131 в книге Оппенгейма & Шафера numer = denom = 0; double sign = 1; for( int i = 0; i <= r; i++ ) { numer += ad[i] * d[ext[i]]; denom += sign * ad[i] / w[ext[i]]; sign = -sign; } final double delta = numer / denom; sign = 1;
// Расчитываем y[] - уравнение 7.133b в книге Оппенгейма & Шафера for( int i = 0; i <= r; i++ ) { y[i] = d[ext[i]] - sign * delta / w[ext[i]]; sign = -sign; } } /********************* * computeA *========== * Используя значения, расчитанные в CalcParms, ComputeA расчитывает * действительный отклик фильтра на заданной частоте (freq). * Используется уравнение 7.133a из книги Оппенгейма & Шафера. * * @param freq - частота (от 0 до 0.5) для которой расчитывается A * @param r - число коэффициентов фильтра / 2 * @param ad - 'b' в книге Оппенгейма & Шафера [r+1] * @param x - [r+1] * @param y - 'C' в книге Оппенгейма & Шафера [r+1] * * @return возвращает значение в виде double для A[freq] *********************/ private static double computeA(double freq, int r, double ad[], double x[], double y[]) { double numer = 0; double denom = 0; final double xc = Math.cos( 2.0 * Math.PI * freq ); for( int i = 0; i <= r; i++ ) { double c = xc - x[i]; if( Math.abs(c) < 1.0e-7 ) { numer = y[i]; denom = 1; break; } c = ad[i] / c; denom += c; numer += c * y[i]; } return numer / denom; } /************************ * calcError *=========== * Расчитывает функцию Ошибки исходя из желаемого частотного отклика * плотной сетки (d[]), весовой функции плотной сетки (w[]), * и имеющегося расчитанного отклика (A[]) * * @param r - число коэффициентов фильтра / 2 * @param ad - [r+1] * @param x - [r+1] * @param y - [r+1] * @param gridSize - число элементов в плотной сетке частот * @param grid - частоты (от 0 до 0.5) плотной сетки [gridSize] * @param d - желаемый отклик плотной сетки [gridSize] * @param w - весовая функция плотной сетки [gridSize] * * @return e - функция ошибки плотной сетки [gridSize] ************************/ private static void calcError(int r, double ad[], double x[], double y[], int gridSize, double grid[], double d[], double w[], double e[]) { for( int i = 0; i < gridSize; i++ ) { final double A = computeA( grid[i], r, ad, x, y ); e[i] = w[i] * (d[i] - A); } } /************************ * search *======== * Ищет максимумы/минимумы огибающей ошибки. Если найден более чем * r+1 экстремум, используется следующая эвристика (спасибо Крису Хансону): * 1) Сначала удаляются прилегающие, не меняющиеся экстремумы. * 2) Если есть более одного лишнего экстремума, удаляем имеющий * наименьшую ошибку. Это позволит создать условия нечередования, * которое устраняется п. 1). * 3) Если есть только один лишний экстремум, удаляем меньший их * первого/последнего экстремума * * @param r - число коэффициентов фильтра / 2 * @param ext - указатели на grid[] экстремальных частот [r+1] * @param gridSize - число элементов в плотной сетке частот * @param e - массив значений ошибки. [gridSize] * * @return ext - новые указатели на экстремальные частоты [r+1] ************************/ private static void search(int r, int ext[], int gridSize, double e[]) { final int[] foundExt = new int[gridSize];// Массив найденных экстремумов int k = 0; // Проверка на экстремум в 0. if( ((e[0] > 0.0) && (e[0] > e[1])) || ((e[0] < 0.0) && (e[0] < e[1])) ) foundExt[k++] = 0;
// Проверка на экстремум внутри плотной сетки for( int i = 1; i < gridSize - 1; i++ ) { if( ((e[i] >= e[i-1]) && (e[i] > e[i+1]) && (e[i] > 0.0)) || ((e[i] <= e[i-1]) && (e[i] < e[i+1]) && (e[i] < 0.0)) ) foundExt[k++] = i; }
// Проверка на экстремум в 0.5 int j = gridSize - 1; if( ((e[j] > 0.0) && (e[j] > e[j-1])) || ((e[j] < 0.0) && (e[j] < e[j-1]))) foundExt[k++] = j;
// Удаление лишних экстремумов for( int extra = k - (r + 1); extra > 0; extra-- ) { boolean up = e[foundExt[0]] > 0.0; // up = true --> первый это максимум // up = false --> первый это минимум int l = 0; boolean alt = true; for( j = 1; j < k; j++ ) { if( Math.abs(e[foundExt[j]]) < Math.abs(e[foundExt[l]]) ) l = j;// новая наименьшая ошибка. if( up && (e[foundExt[j]] < 0.0) ) up = false;// переключение на поиск минимума else if( ! up && (e[foundExt[j]] > 0.0) ) up = true;// переключение на поиск максимума else { alt = false; break;// упс, найдено 2 не попеременных }// экстремум. Удаляем наиментший из них }// когда цикл закончен, все экстремумы являются попеременными
// Если есть только доин лишний экстремум, а все другие попеременные, // удаляем наименьший из первого/последнего экстремума. if( alt && (extra == 1) ) { if( Math.abs(e[foundExt[k-1]]) < Math.abs(e[foundExt[0]]) ) l = foundExt[k - 1];// удаляем последний экстремум else l = foundExt[0];// удаляем первый экстремум }
for( j = l; j < k; j++ )// цикл удаления foundExt[j] = foundExt[j + 1]; k--; } // копируем найденные экстремумы в ext[] for( int i = 0; i <= r; i++ ) ext[i] = foundExt[i]; } /******************* * isDone *======== * Проверяет, достаточно ли мала функция ошибок, чтобы считать, * что результат сошёлся. * * @param r - число коэффициентов фильтра / 2 * @param ext - указатели на экстремальные частоты [r+1] * @param e - функция ошибки плотной сетки [gridSize] * * @return возвращает true, если результат сошёлся, * false, если результат не сошёлся ********************/ private static boolean isDone(int r, int ext[], double e[]) { double min, max; min = max = Math.abs( e[ext[0]] ); for( int i = 1; i <= r; i++ ){ final double current = Math.abs( e[ext[i]] ); if( current < min ) min = current; if( current > max ) max = current; } if( ((max - min) / max) < 0.0001 ) return true; return false; } /********************* * freqSample *============ * Простой алгоритм частотной дискретизации для определения * импульсного отклика h[] из значений A, найденных в ComputeA * * @param A - примерные точки желаемого отклика [N/2] * @param is_symm - симметричность желаемого фильтра * @param N - число коэффициентов фильтра * * @return h - импульсный отклик финального фильтра [N] *********************/ private static void freqSample(double A[], boolean is_symm, final int N, double[] h) { double x, val; final double M = (N - 1.0) / 2.0; if( is_symm ) { if( (N & 1) != 0 ) { for( int n = 0; n < N; n++ ) { val = A[0]; x = 2.0 * Math.PI * (n - M) / N; for( int k = 1; k <= M; k++ ) val += 2.0 * A[k] * Math.cos( x * k ); h[n] = val / N; } } else { for( int n = 0; n < N; n++ ) { val = A[0]; x = 2.0 * Math.PI * (n - M) / N; for( int k = 1; k <= (N / 2 - 1); k++ ) val += 2.0 * A[k] * Math.cos( x * k ); h[n] = val / N; } } } else { if( (N & 1) != 0 ) { for( int n = 0; n < N; n++ ) { val = 0; x = 2.0 * Math.PI * (n - M) / N; for( int k = 1; k <= M; k++ ) val += 2.0 * A[k] * Math.sin( x * k ); h[n] = val / N; } } else { for( int n = 0; n < N; n++ ) { val = A[N / 2] * Math.sin( Math.PI * (n - M) ); x = 2.0 * Math.PI * (n - M) / N; for( int k = 1; k <= (N / 2 - 1); k++ ) val += 2.0 * A[k] * Math.sin( x * k ); h[n] = val / N; } } } } /******************** * remez *======= * Расчёт оптимального (в смысле Чебышева/минимаксного) * импульсного отклика КИХ фильтра, заданного набором границ диапазонов, * желаемого отлика в этих диапазонах и веса ошибки в этих диапазонах. * * @param numtaps - число коэффициентов фильтра * @param numband - число диапазонов в указанном фильтре * @param bands - число границ диапазонов, заданных пользователем [2 * numband] * @param des - заданный пользователем отклик в каждом диапазоне [numband] * @param weight - заданные пользователем веса ошибок [numband] * @param type - тип фильтра * * @return h - импульсный отклик финального фильтра [numtaps] ********************/ private static void remez(int numtaps, double bands[], double des[], double weight[], int type, double[] h) { final boolean is_symmetry = (type == BANDPASS); int r = numtaps >> 1;// число экстремумов if( ((numtaps & 1) != 0) && is_symmetry ) r++;
// Заранее предсказываем размер плотной сетки для размеров массивов int gridSize = 0; int numband = des.length; for( int i = 0; i < numband; i++ ) { gridSize += (int)Math.round( 2.0 * r * GRIDDENSITY * (bands[2 * i + 1] - bands[2 * i]) ); } if( ! is_symmetry ) gridSize--; double[] grid = new double[gridSize]; double[] d = new double[gridSize]; double[] w = new double[gridSize]; double[] e = new double[gridSize]; double[] x = new double[r + 1]; double[] y = new double[r + 1]; double[] ad = new double[r + 1]; double[] taps = new double[r + 1]; int[] ext = new int[r + 1];
// Создаём плотную сетку частот createDenseGrid( r, numtaps, numband, bands, des, weight, gridSize, grid, d, w, is_symmetry ); initialGuess( r, ext, gridSize );
// Для Дифференциатора: (правим сетку) //if( type == DIFFERENTIATOR ) {// не используется // for( int i = 0; i < gridSize; i++ ) { // if( d[i] > 0.0001 ) w[i] /= grid[i]; // } //}
// Для нечётных или несимметричных фильтров, меняем // d[] и w[] в соответствии с алгоритмом Паркса-Маклеллана if( is_symmetry ) { if( (numtaps & 1) == 0 ) { for( int i = 0; i < gridSize; i++ ) { final double c = Math.cos( Math.PI * grid[i] ); d[i] /= c; w[i] *= c; } } } else { if( (numtaps & 1) != 0 ) { for( int i = 0; i < gridSize; i++ ) { final double c = Math.sin( 2.0 * Math.PI * grid[i] ); d[i] /= c; w[i] *= c; } } else { for( int i = 0; i < gridSize; i++ ) { final double c = Math.sin( Math.PI * grid[i] ); d[i] /= c; w[i] *= c; } } } // Выполняем алгоритм обмена Ремеза int iter = 0; for( ; iter < MAXITERATIONS; iter++ ) { calcParms( r, ext, grid, d, w, ad, x, y ); calcError( r, ad, x, y, gridSize, grid, d, w, e ); search( r, ext, gridSize, e ); if( isDone( r, ext, e ) ) break; } if( iter == MAXITERATIONS ) { System.out.println("Reached maximum iteration count."); System.out.println("Results may be bad."); }
calcParms( r, ext, grid, d, w, ad, x, y );
// Ищем 'отводы' фиьтра для использования частотной дискретизации // Для нечётных или несимметричных фильтров корректируем отводы // в соответствии с алгоритмом Паркса-Маклеллана for( int i = 0; i <= numtaps / 2; i++ ) { double c; if( is_symmetry ) { if( (numtaps & 1) != 0 ) c = 1; else c = Math.cos( Math.PI * (double)i / numtaps ); } else { if( (numtaps & 1) != 0 ) c = Math.sin( 2.0 * Math.PI * (double)i / numtaps ); else c = Math.sin( Math.PI * (double)i / numtaps); } taps[i] = computeA( (double)i / numtaps, r, ad, x, y ) * c; } // Расчёт частотной дискретизации используя расчитанные 'отводы' freqSample( taps, is_symmetry, numtaps, h ); } /** * Инициализация параметров для расчёта методом Паркса-Маклеллана * @param type - тип фильтра * @param order - порядок фильтра * @param f1 - частота среза ФНЧ и ФВЧ фильтра * @param f2 - верхняя частота для полосового и режекторного фильтра * @param trband - нормализованная переходная полоса фильтра * @param sampleRate - частота дискретизации * @param atten_dB - степень подавления в дБ. * @param ripple_dB - пульсации в полосе пропускания дБ */ public void init(byte type, int order, float f1, float f2, float trband, float sampleRate, float atten_dB, float ripple_dB) { f1 /= sampleRate; f2 /= sampleRate; trband /= sampleRate; int numBands = 2; final double deltaP = 0.5 * (1.0 - Math.pow( 10.0, -0.05 * ripple_dB ) ); final double deltaS = (float)Math.pow( 10.0, -0.05 * atten_dB ); final double rippleRatio = deltaP / deltaS; // оцениваем необходимый порядок фильтра с помощью формулы Кайзера //if( order < 1 ) order = estimatedOrder( trband, atten, ripple ); //int numTaps = order + 1; if( order < 1 ) order = estimatedOrder( trband, atten_dB, ripple_dB ) + 1; int numTaps = order; if( type == BANDPASS || type == BANDSTOP ) numBands = 3; double[] desired = new double[numBands]; double[] bands = new double[numBands << 1]; double[] weights = new double[numBands]; switch ( type ) { case LOWPASS: desired[0] = 1.0; desired[1] = 0.0; bands[0] = 0.0; bands[1] = f1; bands[2] = f1 + trband; bands[3] = 0.5; weights[0] = 1.0; weights[1] = rippleRatio; break; case HIGHPASS: desired[0] = 0.0; desired[1] = 1.0; bands[0] = 0.0; bands[1] = f1 - trband; bands[2] = f1; bands[3] = 0.5; weights[0] = rippleRatio; weights[1] = 1.0; break; case BANDPASS: desired[0] = 0.0; desired[1] = 1.0; desired[2] = 0.0; bands[0] = 0.0; bands[1] = f1 - trband; bands[2] = f1; bands[3] = f2; bands[4] = f2 + trband; bands[5] = 0.5; weights[0] = rippleRatio; weights[1] = 1.0; weights[2] = rippleRatio; break; case BANDSTOP: desired[0] = 1.0; desired[1] = 0.0; desired[2] = 1.0; bands[0] = 0.0; bands[1] = f1 - trband; bands[2] = f1; bands[3] = f2; bands[4] = f2 + trband; bands[5] = 0.5; weights[0] = 1; weights[1] = rippleRatio; weights[2] = 1; break; } // BANDPASS противоположен DIFFERENTIATOR или HILBERT ! m_fir = new double[numTaps]; remez( numTaps, bands, desired, weights, type==LOWPASS?BANDPASS:type, m_fir ); m_delay = new short[order];// создаём и обнуляем буфер данных } /** * фильтрация * @param sample - отсчёт звука * @return результат фильтрации */ public short proc(short sample) { // линия задержки for( int i = m_delay.length; --i > 0; ) m_delay[i] = m_delay[i - 1]; m_delay[0] = sample; // расчёт отклика double out = 0; for( int i = 0; i < m_delay.length; i++ ) out += m_delay[i] * m_fir[i]; // ограничение амплитуды if( out > 0 ) { out += 0.5; if( out > 32767 ) out = 32767; } else { out -= 0.5; if( out < -32768 ) out = -32768; } return (short)out; } }
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Предыдущая Содержание Следующая |